96. Unique Binary Search Trees
Problem
Given an integer n, return the number of structurally unique BST’s (binary search trees) which has exactly n nodes of unique values from 1 to n.
https://leetcode.com/problems/unique-binary-search-trees/
Example 1:
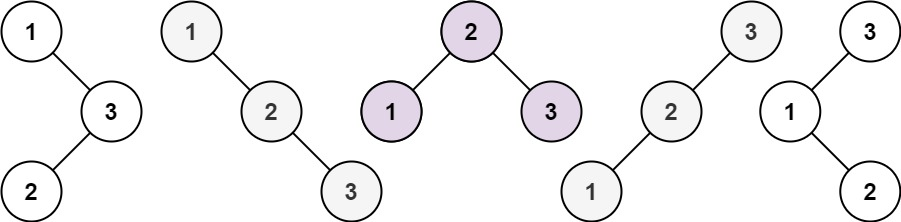
Input: n = 3
Output: 5
Example 2:
Input: n = 1
Output: 1
Constraints:
Test Cases
1
2
| class Solution:
def numTrees(self, n: int) -> int:
|
solution_test.py1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| import pytest
from solution import Solution
from solution2 import Solution as Solution2
@pytest.mark.parametrize('n, expected', [
(3, 5),
(1, 1),
(5, 42),
(19, 1767263190),
])
@pytest.mark.parametrize('sol', [Solution(), Solution2()])
def test_solution(sol, n, expected):
assert sol.numTrees(n) == expected
|
Thoughts
定义 f(i) 表示 1 到 i 所能组成的二叉搜索树的个数。初值 f(0) = 1,题目所求结果为 f(n)。
1 到 i 的每个数字都可以作为根节点。假设以 k 作为根节点,那么左边有 k - 1 个节点,共有 f(k - 1) 种 BSTs;右边有 i - k 个节点,共有 f(i - k) 中 BSTs;所以以 k 为根节点的 BST 共有 f(k - 1) * f(i - k) 个。
所以:
f(i)=k=1∑i{f(k−1)×f(i−k)}
时间复杂度 O(n²),空间复杂度 O(n)。
Code
solution.py1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution:
def numTrees(self, n: int) -> int:
dp = [1] * (n + 1)
for i in range(2, n + 1):
m = i >> 1
cnt = 0
for a in range(m):
cnt += dp[a] * dp[i - 1 - a]
cnt <<= 1
if i & 1:
cnt += dp[m] * dp[m]
dp[i] = cnt
return dp[n]
|
Math
卡塔兰数(Catalan number)的数学定义是:
{C0=1Cn=∑i=1nCi−1Cn−ifor n>0
显然上边定义的 f(n) 就是卡塔兰数(f(n) = Cₙ),可以用数学方法直接计算。
f(n)=Cn=n+11(n2n)=(n+1)!n!(2n)!
本题的 n 不是很大,可以直接用 Python 内置的阶乘函数(math.factorial)计算,时间复杂度 O(n),空间复杂度 O(1)。如果 n 比较大,也可以参考 62. Unique Paths 中的 方法 计算 (n2n)。
solution2.py1
2
3
4
5
6
7
| from math import factorial
class Solution:
def numTrees(self, n: int) -> int:
tmp = factorial(n)
return factorial(n << 1) // tmp // tmp // (n + 1)
|