785. Is Graph Bipartite?

Problem

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u).
There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected).
The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite（二分图） if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

https://leetcode.com/problems/is-graph-bipartite/

Example 1:

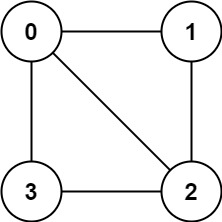
case1

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

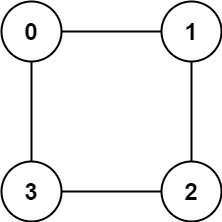
case2

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.

Test Cases

1 2	class Solution: def isBipartite(self, graph: List[List[int]]) -> bool:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('param, expected', [
    ([[1,2,3],[0,2],[0,1,3],[0,2]], False),
    ([[1,3],[0,2],[1,3],[0,2]], True),
])
@pytest.mark.parametrize('sol', [Solution()])
def test_solution(sol, param, expected):
    assert sol.isBipartite(param) == expected

Thoughts

可以尝试给图中所有顶点染色（设有红色和蓝色两种颜色）。如果一个顶点染成红色，那么跟它相邻的顶点就只能染成蓝色，反之亦然。如果存在一个顶点，跟它相邻的顶点中，同时有至少一个红色和至少一个蓝色，图就不是二部图。

任选一个顶点出发对图做遍历（DFS 或 BFS），给相邻的顶点染相对的颜色，如果发现冲突就说明不是二部图。记录已经染过色的顶点的颜色，如果一个连通子图处理完，还有未染色的顶点就再任取一个继续遍历。

Code

solution.py

class Solution:
    def isBipartite(self, graph: list[list[int]]) -> bool:
        n = len(graph)
        colors = [-1] * n

        for u in range(n):
            if colors[u] >= 0: continue
            colors[u] = 0
            stack = [u]
            while stack:
                u = stack.pop()
                cu = colors[u]
                cv = 1 - cu
                for v in graph[u]:
                    if colors[v] == -1:
                        colors[v] = cv
                        stack.append(v)
                    elif colors[v] == cu:
                        return False

        return True