Problem
You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.
Return the minimum number of moves to transform the board into a chessboard board. If the task is impossible, return -1.
A chessboard board is a board where no 0’s and no 1’s are 4-directionally adjacent.
https://leetcode.cn/problems/transform-to-chessboard/
Example 1:
Input:
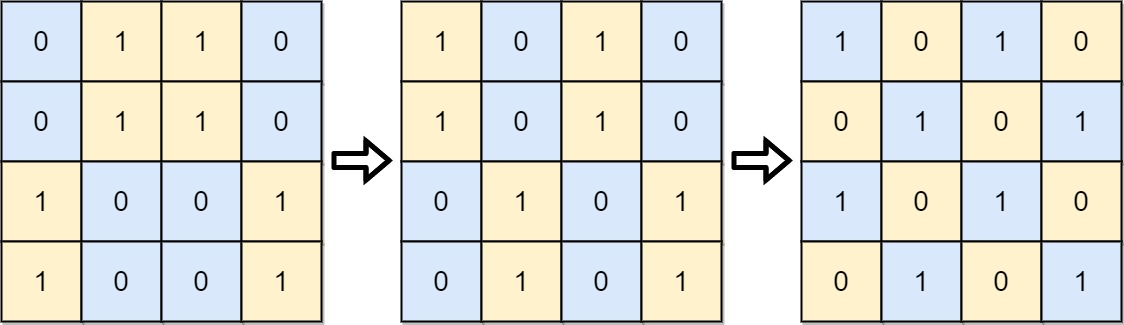
board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
Output:2
Explanation: One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
Example 2:
Input:
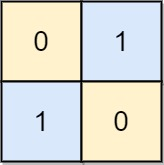
board = [[0,1],[1,0]]
Output:0
Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.
Example 3:

Input:
board = [[1,0],[1,0]]
Output:-1
Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.
Constraints:
n == board.lengthn == board[i].length2 <= n <= 30board[i][j]is either0or1.
Test Cases
1 | class Solution: |
1 | import pytest |
Thoughts
先看第一行。其中 0 的个数和 1 个数必须相等(对于偶数 n)或者刚好相差 1(对于奇数 n),否则就无法变为棋盘。
第一列也是一样的。
然后看后续的每一行,只能有两个可能,要么跟第一行完全一致,要么跟第一行完全互补(0 和 1 互补)。否则也无法变为棋盘。
按照此条件检查完所有行如果成功,所有列也就自动符合相同要求,不用额外检查。
以上条件都符合的话,board 一定可以变为棋盘,否则不行。
再看第一行,看其中不在正确位置的 0 和 1 有多少个,该个数除以 2 就是复原所需要的列交换次数。有个问题是正确的位置应该是什么。
当 n 是奇数时,如果这行中 1 的个数多,则正确的排列是 1 - 0 - 1 - ... - 0 - 1,否则是 0 - 1 - 0 - ... - 1 - 0。
当 n 是偶数时,正确的排列是 0 - 1 - 0 - ... - 0 - 1 或者 1 - 0 - 1 - ... - 1 - 0。两种情况对应的排列错误数量(相加等于 n)取较小的即可。
再用同样方法计算第一列中不在正确位置的 0 和 1 的个数,除以 2 是需要的行交换次数。
最终总共所需的交换次数为 列交换次数 + 行交换次数。
Code
1 | class Solution: |