3249. Count the Number of Good Nodes

Problem

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [aᵢ, bᵢ] indicates that there is an edge between nodes aᵢ and bᵢ in the tree.

A node is good if all the subtrees rooted at its children have the same size.

A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.

Return the number of good nodes in the given tree.

https://leetcode.cn/problems/count-the-number-of-good-nodes/

Example 1:

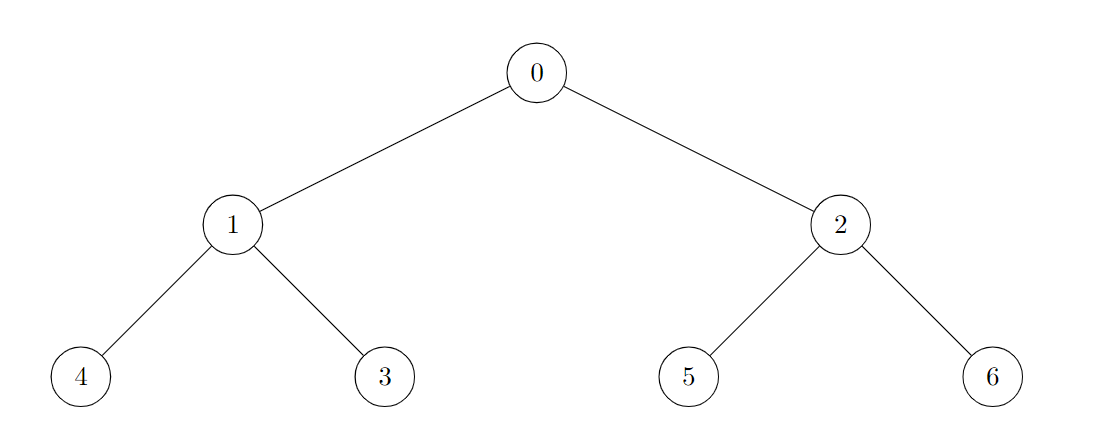
Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: 7
Explanation:

All of the nodes of the given tree are good.

Example 2:

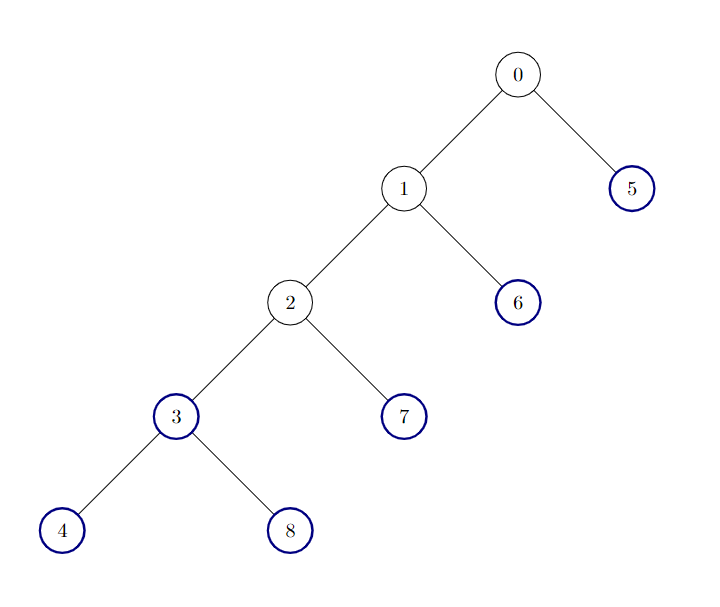
Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
Output: 6
Explanation:

There are 6 good nodes in the given tree. They are colored in the image above.

Example 3:

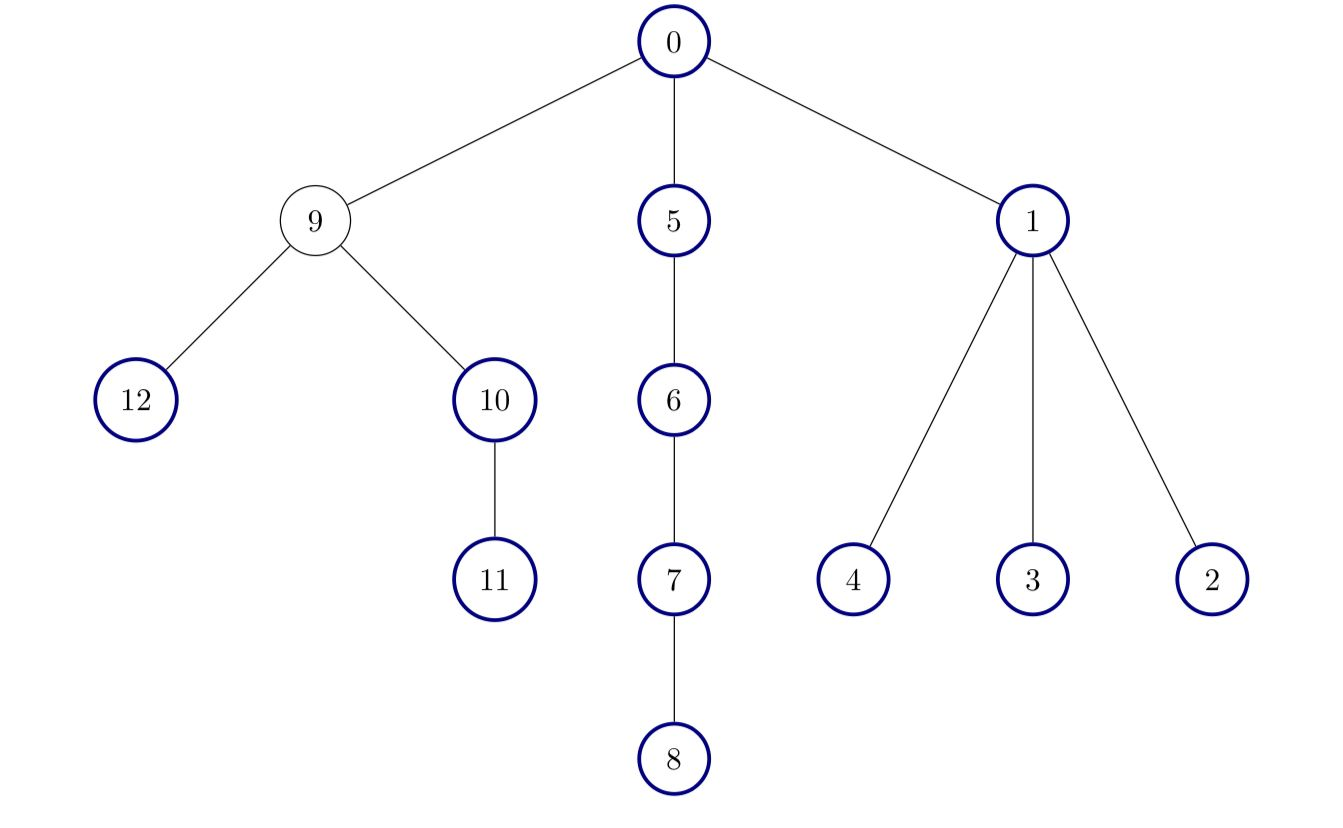
Input: edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]
Output: 12
Explanation:

All nodes except node 9 are good.

Constraints:

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= aᵢ, bᵢ < n
The input is generated such that edges represents a valid tree.

Test Cases

1 2	class Solution: def countGoodNodes(self, edges: List[List[int]]) -> int:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('edges, expected', [
    ([[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], 7),
    ([[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]], 6),
    ([[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]], 12),
])
class Test:
    def test_solution(self, edges, expected):
        sol = Solution()
        assert sol.countGoodNodes(edges) == expected

Thoughts

叶子节点显然是 good，以其为根的 subtree 的节点总数为 1，good 节点总数也是 1。

对于内部节点，先依次计算每个子节点 subtree 的节点总数和 good 节点总数。再根据这些信息判断当前节点是否 good，并累加得到以该节点为根的 subtree 的节点总数和 good 节点总数。

后序遍历整棵树，用栈避免递归调用。因为需要先处理完所有子节点之后再处理父节点，所以如果出栈的是一个尚未处理过内部节点，需要把该节点再次入栈（做适当标记），然后把所有子节点入栈，等子节点都计算完，再对该节点做收尾处理。

另外不用等所有子节点都处理完再判断父节点是否 good 以及累加其 subtree 的节点数和 good 节点数，可以在每处理完一个子节点（第二次出栈）时，就直接把相关信息更新到父节点上。一种方式是给每个节点都附加一份相关信息（节点总数、good 节点总数、是否 good、已知的子节点 subtree 的节点数量），另一种方式是只保留树根到当前节点通路上每个中间节点的信息，后者可以用另外一个栈辅助。

因为输入是边的集合，且不保证边中两个端点的顺序，需要先在内存中构建树。

对于每个节点，记录所有与其相连的边，包含其父节点和所有子节点。在后序遍历时，可以容易地排除掉父节点，只把所有子节点入栈。

需要 O(n) 空间辅助记录树的结构，O(n) 时间复杂度。

Code

solution.py

from typing import List


class Stat:
    def __init__(self, val: int):
        self.val = val
        self.node_count = 1
        self.good_count = 0
        self.good = True
        self.child_node_count: int|None = None


class Solution:
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        n = len(edges) + 1
        nodes = [set() for _ in range(n)] # nodes[i]: its neighbors (parent and children).
        for i, j in edges:
            nodes[i].add(j)
            nodes[j].add(i)

        stats = [Stat(None)]
        tasks = [(0, False)]
        while tasks:
            r, ready = tasks.pop()
            node = Stat(r)
            parent = stats[-1]
            if ready:
                node = stats.pop()
                parent = stats[-1]
            elif r == 0 or len(nodes[r]) > 1: # Non-leaf.
                tasks.append((r, True))
                for c in filter(lambda i: i != parent.val, nodes[r]):
                    tasks.append((c, False))
                stats.append(node)
                continue

            node.good_count += 1 if node.good else 0
            parent.node_count += node.node_count
            parent.good_count += node.good_count
            if parent.child_node_count is not None and node.node_count != parent.child_node_count:
                parent.good = False
            parent.child_node_count = node.node_count

        return stats[0].good_count

本文除了题目描述（Problem）部分之外，其他内容由 Calf 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。