3001. Minimum Moves to Capture The Queen

Problem

There is a 1-indexed 8 x 8 chessboard containing 3 pieces.

You are given 6 integers a, b, c, d, e, and f where:

• (a, b) denotes the position of the white rook.
• (c, d) denotes the position of the white bishop.
• (e, f) denotes the position of the black queen.

Given that you can only move the white pieces, return the minimum number of moves required to capture the black queen.

Note that:

• Rooks can move any number of squares either vertically or horizontally, but cannot jump over other pieces.
• Bishops can move any number of squares diagonally, but cannot jump over other pieces.
• A rook or a bishop can capture the queen if it is located in a square that they can move to.
• The queen does not move.

https://leetcode.cn/problems/minimum-moves-to-capture-the-queen/

Example 1:

Input: a = 1, b = 1, c = 8, d = 8, e = 2, f = 3
Output: 2
Explanation: We can capture the black queen in two moves by moving the white rook to (1, 3) then to (2, 3).
It is impossible to capture the black queen in less than two moves since it is not being attacked by any of the pieces at the beginning.

Example 2:

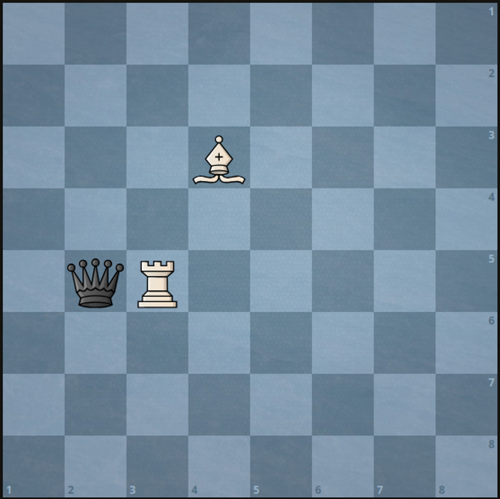
Input: a = 5, b = 3, c = 3, d = 4, e = 5, f = 2
Output: 1
Explanation: We can capture the black queen in a single move by doing one of the following:

• Move the white rook to (5, 2).
• Move the white bishop to (5, 2).

Constraints:

• 1 <= a, b, c, d, e, f <= 8
• No two pieces are on the same square.

Test Cases

1
2

class Solution:
    def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:

1
2
3
4
5
6
7
8
9
10
11
12
13

import pytest

from solution import Solution


@pytest.mark.parametrize('params, expected', [
    ([1, 1, 8, 8, 2, 3], 2),
    ([5, 3, 3, 4, 5, 2], 1),
])
class Test:
    def test_solution(self, params, expected):
        sol = Solution()
        assert sol.minMovesToCaptureTheQueen(*params) == expected

Thoughts

如果没有 bishop，显然 rook 最多两步可以抓到 queen。如果 rook 跟 queen 不在同一行或列，单个 bishop 无法同时挡住 rook 的两条路线，依然是两步杀。如果 rook 跟 queen 在同一行或列，而 bishop 刚好挡在中间，则第一步让 bishop 随便挪走，下一步让 rook 抓到 queen。

所以任何情况最多只需要两步。

一步杀只有两种可能。一种是 rook 跟 queen 在同一行或列，且 bishop 没挡在中间。另一种是 bishop 跟 queen 在同一条斜线（根据 51. N-Queens 可知同一斜线的条件是行列之和相等或之差相等），且 rook 没挡在中间。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution:
    def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:
        # Rook and queen in the same row or col, and bishop not between them.
        if e == a and not (e == c and (b < d < f or b > d > f)):
            return 1
        if f == b and not (f == d and (a < c < e or a > c > e)):
            return 1

        # bishop and queen in the same diagonal line, and rook not between them.
        if e + f == c + d and not (e + f == a + b and (c < a < e or c > a > e)):
            return 1
        if e - f == c - d and not (e - f == a - b and (c < a < e or c > a > e)):
            return 1

        return 2

参考资料

• 本文引用

  • 51. N-Queens

许可协议

本文除了题目描述（Problem）部分之外，其他内容由 Calf 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。

分享文章