2872. Maximum Number of K-Divisible Components

Problem

There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [aᵢ, bᵢ] indicates that there is an edge between nodes aᵢ and bᵢ in the tree.

You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the iᵗʰ node, and an integer k.

A valid split of the tree is obtained by removing any set of edges, possibly empty, from the tree such that the resulting components all have values that are divisible by k, where the value of a connected component is the sum of the values of its nodes.

Return the maximum number of components in any valid split.

https://leetcode.com/problems/maximum-number-of-k-divisible-components/

Example 1:

case1

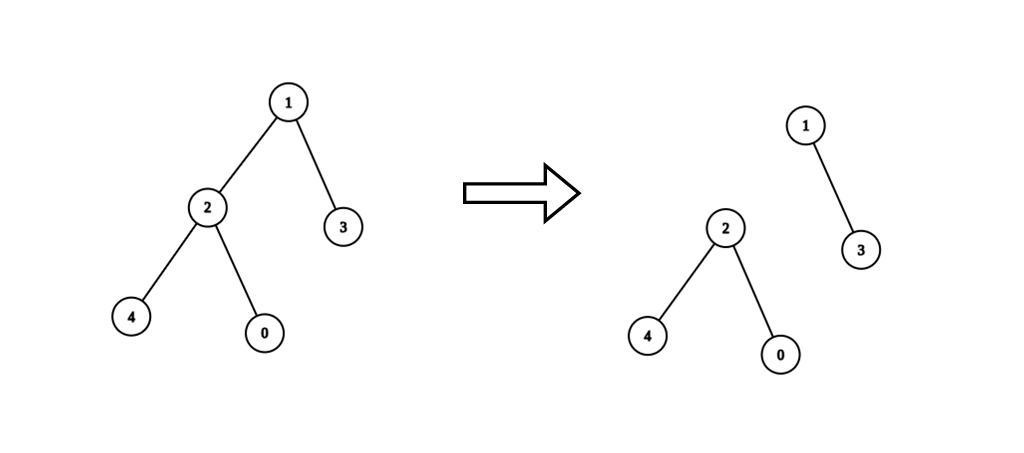
Input: n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6
Output: 2
Explanation: We remove the edge connecting node 1 with 2. The resulting split is valid because:

The value of the component containing nodes 1 and 3 is values[1] + values[3] = 12.

The value of the component containing nodes 0, 2, and 4 is values[0] + values[2] + values[4] = 6.

It can be shown that no other valid split has more than 2 connected components.

Example 2:

case2

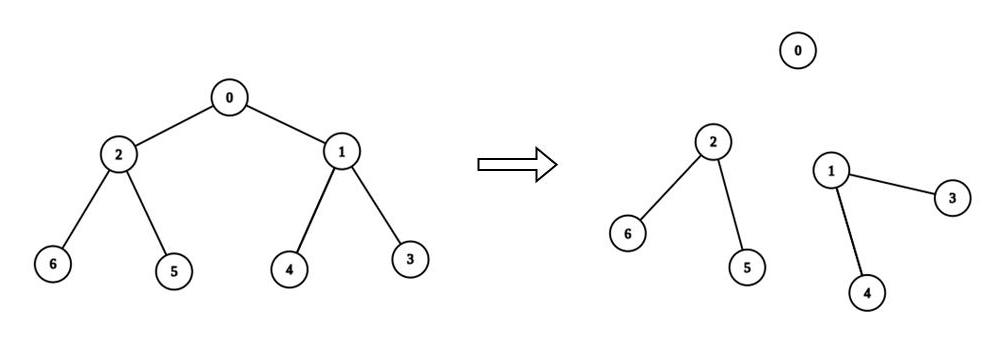
Input: n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3
Output: 3
Explanation: We remove the edge connecting node 0 with 2, and the edge connecting node 0 with 1. The resulting split is valid because:

The value of the component containing node 0 is values[0] = 3.

The value of the component containing nodes 2, 5, and 6 is values[2] + values[5] + values[6] = 9.

The value of the component containing nodes 1, 3, and 4 is values[1] + values[3] + values[4] = 6.

It can be shown that no other valid split has more than 3 connected components.

Constraints:

1 <= n <= 3 * 10⁴
edges.length == n - 1
edges[i].length == 2
0 <= aᵢ, bᵢ < n
values.length == n
0 <= values[i] <= 10⁹
1 <= k <= 10⁹
Sum of values is divisible by k.
The input is generated such that edges represents a valid tree.

Test Cases

1 2	class Solution: def maxKDivisibleComponents(self, n: int, edges: List[List[int]], values: List[int], k: int) -> int:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('n, edges, values, k, expected', [
    (5, [[0,2],[1,2],[1,3],[2,4]], [1,8,1,4,4], 6, 2),
    (7, [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], [3,0,6,1,5,2,1], 3, 3),
])
@pytest.mark.parametrize('sol', [Solution()])
def test_solution(sol, n, edges, values, k, expected):
    assert sol.maxKDivisibleComponents(n, edges, values.copy(), k) == expected

Thoughts

任选一条边，两头各有一棵子树，如果其中一棵子树的节点的 value 之和可以被 k 整除，那么这条边就可以断开。

可以选任意节点作为树根 root。对于某个节点 u，记 s(u) 表示以 u 为根节点的子树的各节点 value 之和。如果 s(u) % k = 0，就可以把以 u 为根节点的子树拆出去成为独立的部分。显然 s(root) % k = 0。所以一共有几个节点的 s 值能被 k 整除，就可以把原树拆分成几个部分，这些节点就是各个独立部分的子树树根（可能只有一个节点）。

问题就转变为，求所有节点的 s 值。可以用后序遍历， $s(u)=\sum_v{s_v}$ ，其中 v 是 u 的所有子节点。

二叉树的后序遍历可以参考 124. Binary Tree Maximum Path Sum 或 337. House Robber III。但是普通的树，每个节点可以有任意多个子节点，就需要在子节点入栈前，把当前节点再次入栈，并附带上标记，当它带着标记出栈的时候，就可以知道它的子节点已经都处理完了。

另外提供的数据中没有明确表明谁是谁的父节点，可以在遍历过程中记录是从哪个节点访问过来的。

时间复杂度 O(n)，空间复杂度 O(n)。

Code

solution.py

class Solution:
    def maxKDivisibleComponents(self, n: int, edges: list[list[int]], values: list[int], k: int) -> int:
        tree = [[] for _ in range(n)] # tree[u]: u's neighbors.
        for u, v in edges:
            tree[u].append(v)
            tree[v].append(u)

        cnt = 0
        stack = [(-1, 0, False)] # (parent, node, children done)
        while stack:
            p, u, ready = stack.pop()
            if ready:
                for v in tree[u]:
                    if v != p: values[u] += values[v]
                if values[u] % k == 0:
                    cnt += 1
            else:
                stack.append((p, u, True))
                for v in tree[u]:
                    if v != p: stack.append((u, v, False))

        return cnt