Problem
You are given an undirected weighted connected graph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [aᵢ, bᵢ, wᵢ] indicates that there is an edge between nodes aᵢ and bᵢ with weight wᵢ.
Some edges have a weight of -1 (wᵢ = -1), while others have a positive weight (wᵢ > 0).
Your task is to modify all edges with a weight of -1 by assigning them positive integer values in the range [1, 2 * 10⁹] so that the shortest distance between the nodes source and destination becomes equal to an integer target. If there are multiple modifications that make the shortest distance between source and destination equal to target, any of them will be considered correct.
Return an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or an empty array if it’s impossible.
Note: You are not allowed to modify the weights of edges with initial positive weights.
https://leetcode.com/problems/modify-graph-edge-weights/
Example 1:
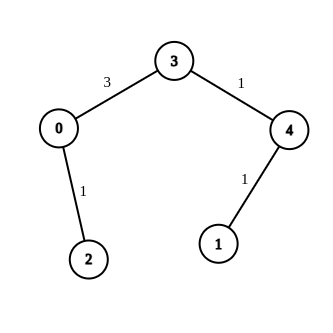
Input:
n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
Output:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
Explanation: The graph above shows a possible modification to the edges, making the distance from0to1equal to 5.
Example 2:
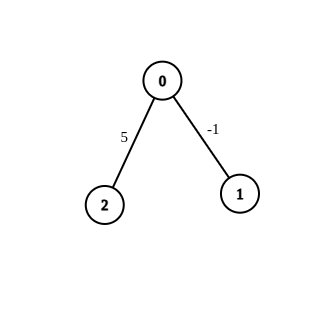
Input:
n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
Output:[]
Explanation: The graph above contains the initial edges. It is not possible to make the distance from0to2equal to 6 by modifying the edge with weight -1. So, an empty array is returned.
Example 3:
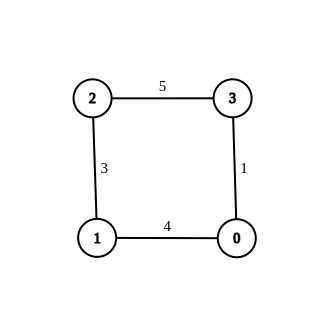
Input:
n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
Output:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
Explanation: The graph above shows a modified graph having the shortest distance from0to2as 6.
Constraints:
1 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= aᵢ, bᵢ < nwᵢ = -1or1 <= wᵢ <= 10⁷aᵢ != bᵢ0 <= source, destination < nsource != destination1 <= target <= 10⁹- The graph is connected, and there are no self-loops or repeated edges
Test Cases
1 | class Solution: |
1 | from collections import defaultdict |
Thoughts
先要实现一番测试代码,因为结果的不确定性,需要单独验证结果是否正确。在测试代码中用 Dijkstra 算法对
Solution.modifiedGraphEdges返回的边的信息,计算source到destination的最短距离,看是不是刚好等于target。
首先假设那些权重为 -1 的边(简称「-1 边」)都不存在,调用 Dijkstra 算法计算 source 到 destination 的最短距离,记为 dist(不通则为 ∞)。显然如果 dist < target,那就无解(类似于 Example 2),直接返回空数组。如果 dist = target 那就不需要做任何有意义的修改(当然题目要求所有 -1 边都必须改成 [1, 2 * 10⁹] 内的正数,那就全都改成 2 * 10⁹ 即可)。如果 dist > target 但是 edges 中没有 -1 边,也无解,直接返回空数组。
Dijkstra 算法的更多信息在 2290. Minimum Obstacle Removal to Reach Corner 有提到。
然后把所有 -1 边的权重都临时改为 1,再调用 Dijkstra 算法计算 source 到 destination 的最短距离,同样记为 dist。如果 dist > target 说明怎么改都无法把最短距离缩减到 target,直接返回空数组。如果 dist = target,那么把最短路径上所有 -1 边的权重都改为 1(同时按题目要求把其他 -1 边的权重改成 2 * 10⁹)即可。
如果 dist < target 就会麻烦一些。一个想法是令 gap = target - dist,在最短路径上任选一条 -1 边,将其权重改为 1 + gap(其他的都改为 1)。但这样改完之后,source 到 destination 的最短路径可能会变化,导致最短距离变得小于 target,比如下面这个情况(source = 0, destination = 3, target = 10):
把所有 -1 边的权重改成 1 之后,找到最短路径 0 - 1 - 2 - 3(蓝色),距离为 dist = 3。如果把 target - dist = 7 随机地加到了边 (1, 2) 上,就会导致最短路径变成 0 - 1 - 3(红色),距离为 6,小于 target 了。
可以按最新的权重重新计算 source 到 destination 的最短距离,如果得到了比 target 小的最短距离,就再任选一条 -1 边,把新的到 gap 加上去。比如上图中,新的 gap 值为 4,任选一条红色路径上的 -1 边(如 (0, 1)),把 4 加上去,得到下图的结果:
重复这一操作直到最短距离等于 target。
所以至少需要做两次 Dijkstra 最短路径计算,时间是 O((E + n) log n)(其中 E 是 edges 的长度)。但是在调整 -1 边权重的时候,最坏情况可能会需要重新计算 O(n) 次最短路径,总的时间复杂度为 O(n (E + n) log n),约等于 O(n³ log n)(因为 O(E) ≈ O(n²))。空间复杂度 O(E)。
提交之后运行时间还可以,97+%。
还有一个调整权重的方法,对于一条在最短路径上的 -1 边 (u, v),取 source 到 u 的最短距离 dist1,和 v 到 destination 的最短距离 dist2,那么把 (u, v) 的权重改成 target - dist1 - dist2。但是这个操作不能连续执行,修改完一条 -1 边的权重之后,对于另外一条 -1 边 (u', v'),需要重新计算 dist1' 和 dist2',复杂度是差不多的。
Code
1 | from collections import defaultdict |