2577. Minimum Time to Visit a Cell In a Grid

Problem

You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].

You are standing in the top-left cell of the matrix in the 0ᵗʰ second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.

Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.

https://leetcode.com/problems/minimum-time-to-visit-a-cell-in-a-grid/

Example 1:

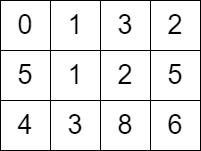
case1

Input: grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
Output: 7
Explanation: One of the paths that we can take is the following:

at t = 0, we are on the cell (0,0).

at t = 1, we move to the cell (0,1). It is possible because grid[0][1] <= 1.

at t = 2, we move to the cell (1,1). It is possible because grid[1][1] <= 2.

at t = 3, we move to the cell (1,2). It is possible because grid[1][2] <= 3.

at t = 4, we move to the cell (1,1). It is possible because grid[1][1] <= 4.

at t = 5, we move to the cell (1,2). It is possible because grid[1][2] <= 5.

at t = 6, we move to the cell (1,3). It is possible because grid[1][3] <= 6.

at t = 7, we move to the cell (2,3). It is possible because grid[2][3] <= 7.
The final time is 7. It can be shown that it is the minimum time possible.

Example 2:

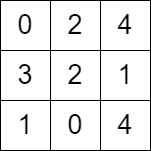
case2

Input: grid = [[0,2,4],[3,2,1],[1,0,4]]
Output: -1
Explanation: There is no path from the top left to the bottom-right cell.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
0 <= grid[i][j] <= 10⁵
grid[0][0] == 0

Test Cases

1 2	class Solution: def minimumTime(self, grid: List[List[int]]) -> int:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('grid, expected', [
    ([[0,1,3,2],[5,1,2,5],[4,3,8,6]], 7),
    ([[0,2,4],[3,2,1],[1,0,4]], -1),

    ([[0,1,99,99],[99,1,2,5],[99,99,99,6]], 7),
    ([[0,1,99,2],[5,1,2,5],[4,3,8,6]], 7),
])
class Test:
    def test_solution(self, grid, expected):
        sol = Solution()
        assert sol.minimumTime(grid) == expected

Thoughts

跟 2290. Minimum Obstacle Removal to Reach Corner 很像，就是边的权重定义不一样。

首先如果 grid[0][1] 和 grid[1][0] 都大于 1 就无解，因为第一步就没得走。

以每个格子作为顶点，上下左右相邻的格子之间作边，作有权无向图。

因为能不能移动到某个格子，跟到达的时间有关，所以边的权重也不是静态的，而是跟访问这条边的时间有关。

设在 t 秒时位于格子 u，看如何能移动到 u 周围的其他格子。取 u 上下左右的某个格子 v，如果 v 的值小于等于 t + 1，那么可以直接移动过去，且到达的时间即为 t + 1。否则就不能直接走到 v，但是可以在 u 和进入 u 之前的那个格子之间来回移动消耗时间，直到 t' + 1 >= grid[v]。因为每次来回都是用 2 秒，所以可以走到 v 的最早时间是 grid[v] 或 grid[v] + 1（取决于 grid[v] - t 的奇偶性）。

直接用 Dijkstra 算法，在 problem 2290 代码的基础上改造一下从 u 移动到 v 之后，v 的到达时间（等价于距离）的计算逻辑。

时间复杂度同样是 O(m*n log (m*n))。

Code

solution.py

from heapq import heappop, heappush
from math import inf


class Solution:
    def minimumTime(self, grid: list[list[int]]) -> int:
        if grid[0][1] > 1 and grid[1][0] > 1:
            return -1

        dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        m = len(grid)
        n = len(grid[0])
        # times[i][j]: the time from [0][0] to [i][j].
        times: list[list[int]] = [[inf] * n for _ in range(m)]

        # Dijkstra.
        times[0][0] = 0
        queue = [(0, 0, 0)] # A min-heap queue of (times[i][j], i, j)
        while queue:
            # Get the best start vertex u = (ui, uj).
            time, ui, uj = heappop(queue)
            if ui == m - 1 and uj == n - 1:
                return time
            elif time > times[ui][uj]: # Pruning.
                continue

            # Update u's adjacent vertices' distances.
            time += 1
            for di, dj in dirs:
                vi = ui + di
                vj = uj + dj
                if 0 <= vi < m and 0 <= vj < n:
                    time_v = time if grid[vi][vj] <= time else grid[vi][vj] + ((grid[vi][vj] - time) & 1)
                    if time_v < times[vi][vj]:
                        times[vi][vj] = time_v
                        heappush(queue, (time_v, vi, vj))