2218. Maximum Value of K Coins From Piles

Problem

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the iᵗʰ pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

https://leetcode.cn/problems/maximum-value-of-k-coins-from-piles/

Example 1:

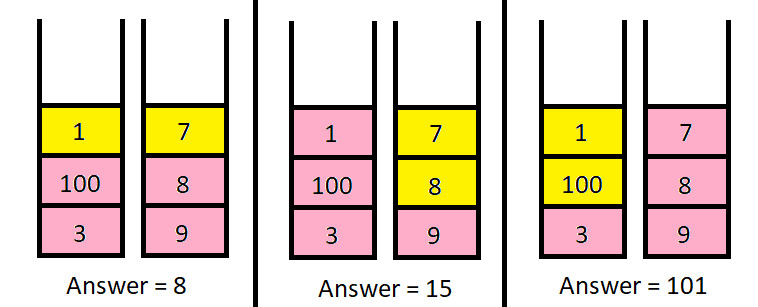
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 10⁵
1 <= k <= sum(piles[i].length) <= 2000

Test Cases

1 2	class Solution: def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('piles, k, expected', [
    ([[1,100,3],[7,8,9]], 2, 101),
    ([[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], 7, 706),
])
@pytest.mark.parametrize('sol', [Solution()])
def test_solution(sol, piles, k, expected):
    assert sol.maxValueOfCoins(piles.copy(), k) == expected

Thoughts

记 dp(p, j) 表示从 piles[0...p] 中选取刚好 j 枚硬币（0 ≤ p < n，1 ≤ j ≤ k），可以得到的最大总额。

先不考虑边界情况（即假设每个 pile 都有足够多的硬币），显然有：

dp(p,j)=\max_{0\le i\le j}{\left\{dp(p-1,j-i)+\sum{piles[p][:i]}\right\}}

初值 dp(-1, j) = 0，dp(p, 0) = 0。最终结果为 dp(n-1, k)。

即从 piles[p] 取 i 枚硬币（0 ≤ i ≤ j），剩余的 j - i 枚从 piles[0...p-1] 取。

一个明显的优化是计算从 piles[p] 取 i 枚硬币的总额，并不需要对于所有的 i 都从 0 开始累加，只需要先计算一遍前缀和，然后直接利用 piles[p] 的空间存储前缀和。即更新后的 piles'[p][i] = Σpiles[p][0...i]，可得：

dp(p,j)=\max\begin{cases} dp(p-1,j) \\ \max_{0\le i<j}{\left\{dp(p-1,j-i-1)+piles'[p][i]\right\}} \end{cases}

计算 dp(p, j) 时只用到 dp(p-1, *)，可以只保留最新的 p 对应的 dp 值。

时间复杂度 O(n * k²)，空间复杂度 O(k)。

考虑到边界条件，可以有一些小优化。比如 piles[0...p] 包含的硬币总数比 k 小，则只需要计算到硬币总数，不需要计算到 k。如果 piles[p] 的硬币数大于 k，则只需要计算前 k 项的前缀和。对于任意 j，如果 piles[p] 的硬币数小于 j，则 $max_{0\le i\le j}$ 这一项的上限可以只取到硬币数。

Code

solution.py

class Solution:
    def maxValueOfCoins(self, piles: list[list[int]], k: int) -> int:
        min2 = lambda a, b: a if a <= b else b
        max2 = lambda a, b: a if a >= b else b

        dp = [0] * (k + 1)
        cnt = 0
        for pile in piles:
            cnt = min2(cnt + len(pile), k)
            for i in range(1, min2(k, len(pile))):
                pile[i] += pile[i-1]

            for j in range(cnt, 0, -1):
                for i in range(min2(j, len(pile))):
                    dp[j] = max2(dp[j], dp[j-i-1] + pile[i])

        return dp[k]

本文除了题目描述（Problem）部分之外，其他内容由 Calf 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。