141. Linked List Cycle

Problem

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

https://leetcode.com/problems/linked-list-cycle/

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

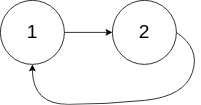
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10^4].
-10^5 <= Node.val <= 10^5
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Test Cases

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:

solution_test.py

import pytest

from node import ListNode
from solution import Solution


def build_linked_list(values, pos):
    tail = None
    root = ListNode(0) # root's next points to the real head.
    node = root
    for i, val in enumerate(values):
        node.next = node = ListNode(val)
        if pos == i:
            tail = node

    node.next = tail
    return root.next


@pytest.mark.parametrize('values, pos, expected', [
    ([3,2,0,-4], 1, True),
    ([1,2], 0, True),
    ([1], -1, False),
])
class Test:
    def test_solution(self, values, pos, expected):
        head = build_linked_list(values, pos)
        sol = Solution()
        assert sol.hasCycle(head) == expected

Thoughts

经典问题，用两个步长不等的指针遍历链表。如果没有环，较快的指针会先走到链表末尾。如果有环，二者一定会相遇。

空间复杂度 O(1)。

设指针 p1 步长为 1，p2 步长为 2。如果链表有环，易知 p1 在环里转满一圈之前，必然会与 p2 相遇。

设环长为 m。p1 进入环时，p2 在 p1 前方第 k 个节点处（0 < k < m）。设经过 s 次移动，p1 和 p2 相遇，显然有 $0+s\equiv k+2s\pmod{m}$ ，易得 s = m - k。

所以时间复杂度是 O(n)。

Code

solution.py

from typing import Optional

from node import ListNode


# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        p1 = p2 = head
        while p2 and p2.next:
            p1 = p1.next
            p2 = p2.next.next
            if p1 == p2:
                return True

        return False

本文除了题目描述（Problem）部分之外，其他内容由 Calf 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。