1368. Minimum Cost to Make at Least One Valid Path in a Grid

Problem

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/

Example 1:

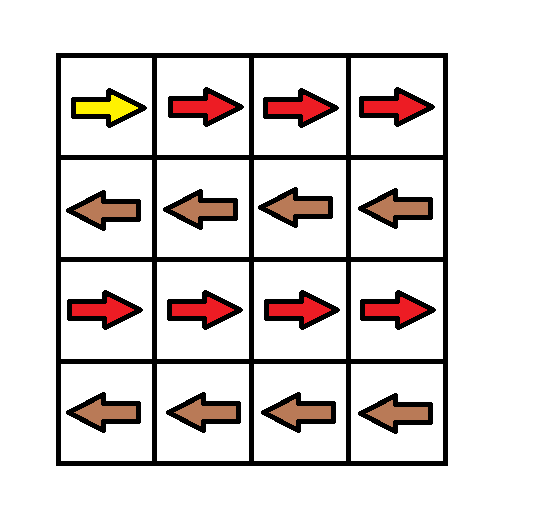
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

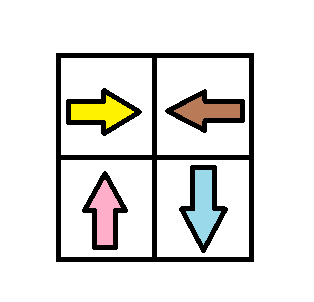
Input: grid = [[1,2],[4,3]]
Output: 1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 4

Test Cases

1 2	class Solution: def minCost(self, grid: List[List[int]]) -> int:

solution_test.py

import pytest

from solution import Solution


@pytest.mark.parametrize('grid, expected', [
    ([[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]], 3),
    ([[1,1,3],[3,2,2],[1,1,4]], 0),
    ([[1,2],[4,3]], 1),
])
@pytest.mark.parametrize('sol', [Solution()])
def test_solution(sol, grid, expected):
    assert sol.minCost(grid) == expected

Thoughts

跟 2290. Minimum Obstacle Removal to Reach Corner 和 2577. Minimum Time to Visit a Cell In a Grid 类似，定义好边的权重即可。

如果边 (u, v) 的方向跟格子 u 的箭头方向一致，则权重为 0，否则权重为 1。

然后用 Dijkstra 算法计算左上角顶点到右下角顶点的最短距离，此距离即为所求 cost。

时间复杂度同样是 O(m*n log (m*n))。

Code

solution.py

from heapq import heappop, heappush
from math import inf


class Solution:
    def minCost(self, grid: list[list[int]]) -> int:
        dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)] # Right, left, down, up.
        m = len(grid)
        n = len(grid[0])
        # dists[i][j] is the distance from (0, 0) to (i, j).
        dists: list[list[int]] = [[inf] * n for _ in range(m)]

        # Dijkstra's algorithm.
        dists[0][0] = 0
        queue = [(0, 0, 0)] # A min-heap queue of (dists[i][j], i, j).
        while queue:
            # Get the best start vertex u = (ui, uj).
            dist, ui, uj = heappop(queue)
            if ui == m - 1 and uj == n - 1:
                return dist
            elif dists[ui][uj] < dist:
                continue

            for k, (di, dj) in enumerate(dirs, 1):
                vi, vj = ui + di, uj + dj
                if 0 <= vi < m and 0 <= vj < n:
                    new_dist = dist + (grid[ui][uj] != k)
                    if new_dist < dists[vi][vj]:
                        dists[vi][vj] = new_dist
                        heappush(queue, (new_dist, vi, vj))