Calf 的三阶魔方复原方法

高中毕业的暑假，自己琢磨出来的魔方复原方法，不用背公式。当然最后几步是固定的套路，可以稍微记一下，记不住就不停地把各种套路都试一试，也可以搞定。

当时的笔记

整体复原流程

① 从一个角出发逐渐往外扩，直到这三个面都只剩下最边缘的角未完成（不需要公式）。把魔方整体转 180°，可以看到对面未完成的部分也只剩下一个倒 Y 形区域（一个中央角块即出发角块的对顶角，三个棱块，三个边缘角块）。

这部分没有公式，就灵活运用躲避的技巧即可。前提是可以非常轻松地完成单面的复原，理解单面复原时最后一步的精髓。

② 把三个边缘角块归位即完成三个面复原，然后再把三个棱块归位便完成了整个复原。

这个阶段，可以做的操作就非常有限，不能随便乱拧了。关键问题在于找到并了解可能的操作组，每组操作都是一个原子单位，操作完不会引入不可预估的破坏，但又能让尚未完成的部分有所进展。

复原三面之前的一些操作

关键就是要善于「躲避」，借助适当的「躲避」操作，可以在一组操作完成之后，已经复原的部分不会受到破坏，但有一定的进展。

状态 4 ⇒ 状态 5

这个阶段要逐个归位出发角对应的三个面（上边图中的红、黄、蓝）各自的棱块。

动画演示

注意看一组操作完成之后，除了多归位了一个黄色面的棱块，其他几个棱块都完全不受影响（只有倒 Y 形区域会发生变化，但现在不用考虑它们，动画中全部涂为灰色减少干扰）。

情形一

情形二

复原三面到六面用的标记 & 操作组

记号说明

虽然算不上公式，但还是需要借助一定的符号体系来描述操作组，需要记忆的无非就是在什么情况下要执行哪些操作组。如果不记忆，把可行的操作组按照各种顺序排列组合，也很容易能蒙对的，只是要慢得多。

将倒 Y 形区域标记为 o-abc 直角坐标系：

axis

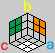
虽然图中标记了各面的颜色（看不见的 a、b、c 面用字母颜色指代），但这只是用于示意的特例，并不是固定的搭配。

如果熟悉传统魔方公式符号，可以假设手持魔方时，让 a、b 夹住的面（图中的橙色面）冲着自己（即 front），a 面（图中蓝色）为 right，b 面（图中黄色）为 top，由此图中绿色面为 left，白色面为 down，看不到的 c 面（图中红色）为 back。

基本操作 `ab`、`ba`

当魔方只剩下倒 Y 形区域没复原的时候，自由度就极低了，一般可以做的操作只有一组（及其逆操作），称其为 ab（逆操作为 ba）。操作组与传统公式体系的对应关系示意：

ab 相当于 D' L D L'
ba 相当于 L D' L' D —— 可见 ab 和 ba 是互逆的

动画演示

以上边图中的颜色对应关系为例，即 a 为蓝色面，b 为黄色面。ab 也可以叫做 蓝黄，ba 可以叫做 黄蓝。

ab 操作（操作时视角）

ab 操作（倒 Y 视角）

ba 操作（操作时视角）

ba 操作（倒 Y 视角）

除了 ab 和 ba 互逆之外，还有个特点是一个操作组连续做六次，就完全回到初始状态。

动画演示

ab x 6

ba x 6

衍生操作 `bc`、`cb`、`ca`、`ac`

由于对称性，其实还有其他的组合，如 bc（逆操作为 cb）、ca（逆操作为 ac）。实际操作的时候，会把魔方摆成让操作组中涉及到的两个面分别在 top 和 right 位置，这样操作最顺手。

跟传统魔方公式不同，他们往往要求不要在手中随意改变魔方的方位，一般至少 top、down 两个面是固定的。但这里的操作组没有这个限制，因为倒 Y 形结构很容易找到，绕着原点 o 怎么调整魔方的方位都是可以的，主要看怎么转着顺手。

动画演示

先对魔方做一次传统公式的 y' z，b 面、c 面就会换到之前 a 面、b 面的位置。

bc 操作

cb 操作

先对魔方做一次传统公式的 z' y，c 面、a 面就会换到之前 a 面、b 面的位置。

ca 操作

ac 操作

特殊操作

前面的那几组操作，核心逻辑都是一致的，每组四次转动，只会改变倒 Y 形区域内的分布，其他区域是完全没有破坏的。

有个别特殊场景，需要刻意（临时地）破坏掉已经复原好其他部分，如：

b'a 相当于 L' D' L D
b 相当于 L

由于对称性，还可以有 c'b、c、a'c、a 等，不再赘述。

动画演示

b'a 操作

b 操作

复原三面

基本思路是先盯住任意两个面，让这两个面同时达到复原的状态，再看第三个面的情况。

不同情况的处理步骤示例（由于对称性，其他情况可以旋转魔方，变更 a、b、c 三面跟颜色的对应关系）。

① 保持两个面不变，调整第三个面的角的朝向

以 b 面为例，它的角在正确的位置，但没在正确的方向。

3-1

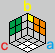
操作方法：ab ab bc bc（a、c 两面完全不变）。

动画演示

② 同上，但方向相反

跟上一种类似，只是方向相反，复原操作是对称的。

3-2

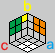
操作方法：cb cb ba ba（a、c 两面完全不变）。

动画演示

③ 交换 `o` 点和面的角

这是整个复原过程中最复杂的情况，当时以及之后的很多年一直都没有完全吃透。它无法单纯依靠基本操作组的排列组合完成复原，必须借助前边提到的特殊操作。

以 c 面为例，它的角在倒 Y 形区域的 o 点那里，而 a、b 面的角都在正确的位置（方向无所谓）。

2-1

2-2

2-3

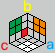
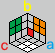
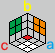
操作方法：b'a b ba，再恢复 b 面的棱（这是一次刻意破坏再重建的过程）。

这两步之后并不会直接达到三面都复原了的状态，但可以根据魔方的实际状态，结合前边提到的两种情况的处理方法，灵活运用基本操作组继续复原。下边动画演示部分，会给出一个相对固定的复原套路，但没必要背下来。

动画演示

以第一张图示意的情况为例。

先做 b'a b ba

再恢复 b（黄色）面的棱

再转好的 a、b（蓝、黄色）两面（示意，倒 Y 视角）

复原六面

不同情况的处理步骤示例。

① 三个棱逆时针归位

6-1

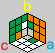
ba cb ac，这时原本好的三面会被破坏，再继续观察并按复原三面的方法对 a、b、c 三面进行复原即可。

动画演示

ba cb ac（倒 Y 视角）

继续复原示意（倒 Y 视角）

② 三个棱顺时针归位

6-2

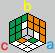
ab ca bc，再继续观察并转好 a、b、c。

动画演示

ab ca bc（倒 Y 视角）

继续复原示意（倒 Y 视角）

③ o-a 棱和 o-b 棱各自原地翻转

6-3

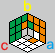
ab ab ca ca，再继续观察并转好 a、b、c。

动画演示

ab ab ca ca（倒 Y 视角）

继续复原示意（倒 Y 视角）

速查表 / 一图流

事项	操作	说明 / 后续
倒 Y 形区域		o-abc 直角坐标系 a 蓝 right b 黄 top c 红 back
基本操作 `ab`	`D' L D L'`	蓝黄
基本操作 `ba`	`L D' L' D`	黄蓝
特殊操作 `b'a`	`L' D' L D`	黄’蓝
特殊操作 `b`	`L`	黄
三① 角的朝向	`ab ab bc bc`	a、c 两面完全不变
三② 角的朝向	`cb cb ba ba`	a、c 两面完全不变
三③ 交换 `o` 和角	`b'a b ba`	再恢复 b 面的棱再复原 a、b、c
六① 三棱逆时针归位	`ba cb ac`	再复原 a、b、c
六② 三棱顺时针归位	`ab ca bc`	再复原 a、b、c
六③ o-a、o-b 棱原地翻转	`ab ab ca ca`	再复原 a、b、c